VOLUME DO PARALELEPÍPEDO,DO CUBO E DO CONE.

O cálculo do volume de cada sólido possui suas particularidades, assim como ocorre no cálculo do volume do Paralelepípedo, do Cubo e do Cone.

 
Aprenda a calcular o volume do paralelepípedo retangular, do cubo e do cone circular reto

Quando falamos sobre volume de um sólido, estamos nos referindo à capacidade desse sólido. Veremos a seguir como calcular o volume do paralelepípedo, docubo e do cone circular reto. Vale a pena ressaltar que, ao calcular o volume de um sólido, é necessário que todas as suas medidas possuam a mesma notação. Por exemplo, se uma das medidas está em centímetros e a outra é dada em metros, é necessário transformar uma delas para torná-la igual às demais.

Um paralelepípedo retangular é um sólido de seis lados que possui faces retangulares planas e paralelas. Tente imaginar o paralelepípedo abaixo como uma piscina. Se nós queremos saber a capacidade dele, é o mesmo que dizer que queremos descobrir quanta água cabe nele. Para chegarmos a uma resposta, precisaremos analisar alguns dados desse sólido, como a largura e o comprimento do retângulo da base, bem como a altura ou profundidade.

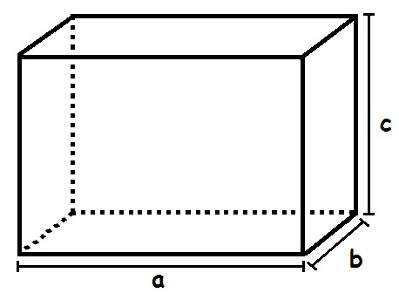
Para calcular o volume desse paralelepípedo, devemos multiplicar as medidas identificadas por a, b e c

Portanto, para calcular o volume do paralelepípedo, temos a seguinte fórmula:

V = a . b . c

Se considerarmos um paralelepípedo em que a largura da base meça 10 m, o comprimento da base, 5 m, e a altura do paralelepípedo meça 8 m, teremos o seguinte volume:

V = (10 m) . (5 m) . (8 m)

V = 400 m³

Temos um tipo especial de paralelepípedo retângulo, o cubo — um sólido com seis faces quadradas e com os mesmos comprimentos de lado. Temos abaixo um cubo cujas arestas medem a.

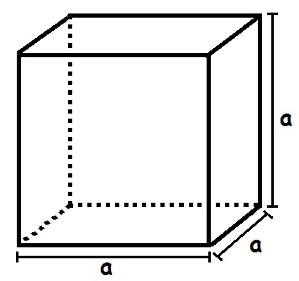
Para calcular o volume do cubo, devemos multiplicar a medida da aresta elevada à terceira potência

Para calcular o volume do cubo, vamos multiplicar as arestas, de modo que faremos a terceira potência dessa aresta:

V = a . a . a

V = a³

Se dissermos, por exemplo, que a aresta desse cubo mede 3 m, o volume dele será:

V = (3m)³

v = 27 m³

Outro sólido que analisaremos é o cone circular reto. Esse sólido tem por características uma base circular de raio r, uma altura h, que forma um ângulo reto com a base, e uma geratriz g. A geratriz de um cone é o segmento de reta que liga o topo da altura às extremidades da base. Na figura a seguir, conseguimos ver com mais facilidade cada uma dessas estruturas:

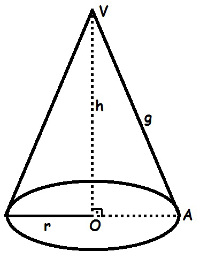
Para calcular o volume do cone circular reto, devemos multiplicar a altura por π e pelo quadrado do raio, bem como dividir o resultado por 3

Para calcularmos a área do cone circular reto, faremos:

V = ⅓ π.r².h

Considere um cone cuja base tem raio 2 m e a altura mede 8 m. Considere π = 3,14. Calculemos o volume do cone:

V = ⅓ π.r².h

                                                                       V =   1   . 3,14 . 2² . 8
                                                                               3

V = 3,14 . 4 . 8
      3

V = 100,48
        3

V ≈ 33,49 m³

Então o volume do cone é de, aproximadamente, 33,49 m³.

Suponha agora que temos um cone circular reto em que a geratriz mede 5 m e a altura, 4 m. Para calcularmos o volume desse sólido, precisamos encontrar a medida do raio, para tanto, utilizaremos o Teorema de Pitágoras:

g² = h² + r²

r² = g² – h²

r² = 5² – 4²

r² = 25 – 16

r² = 9

r = 3 m

Agora que temos o valor do raio, podemos calcular o volume do cone utilizando a fórmula:

V = ⅓ π.r².h

                                                                     V =   1  . 3,14 . 3² . 4
                                                                              3

V = 3,14 . 9 . 4
      3

V = 113,04
        3

V = 37,68 m³

Portanto, o volume desse cone circular reto é 37, 68 m³.

Por Amanda Gonçalves
​Graduada em Matemática/CBM